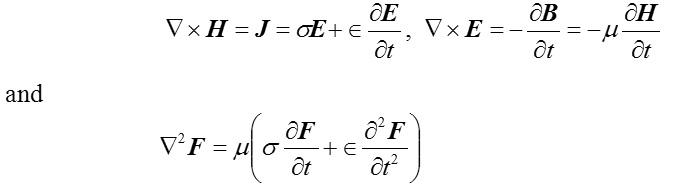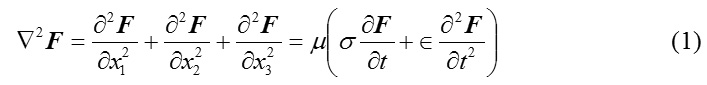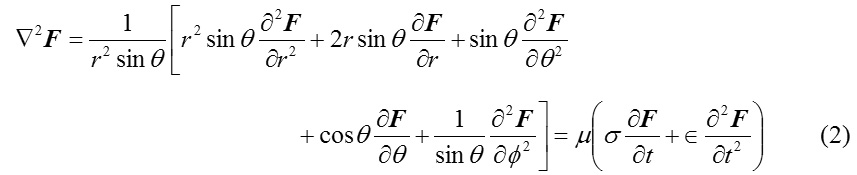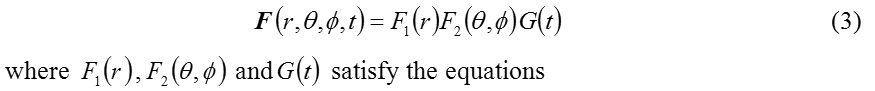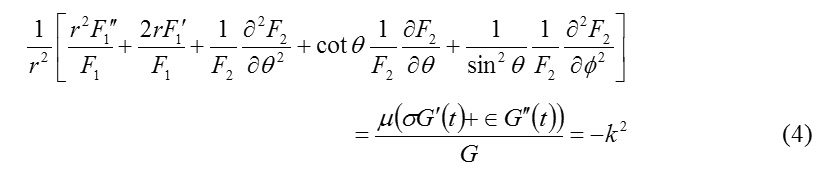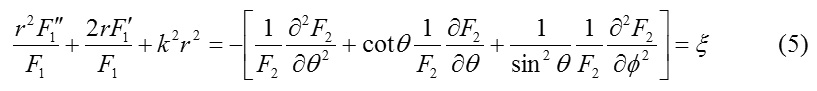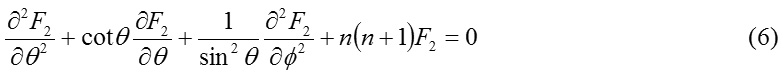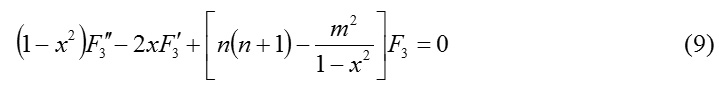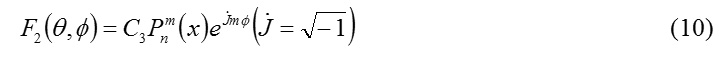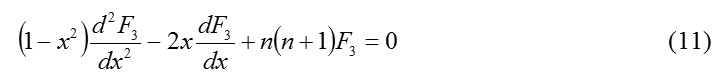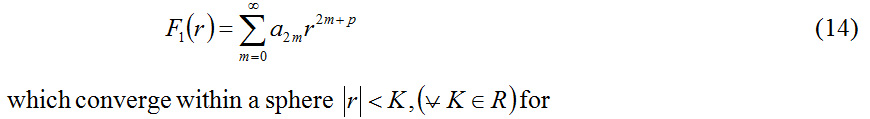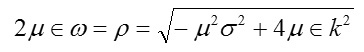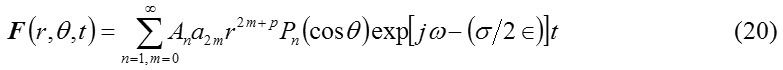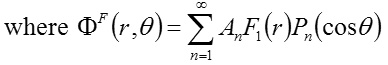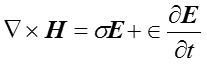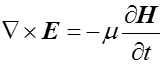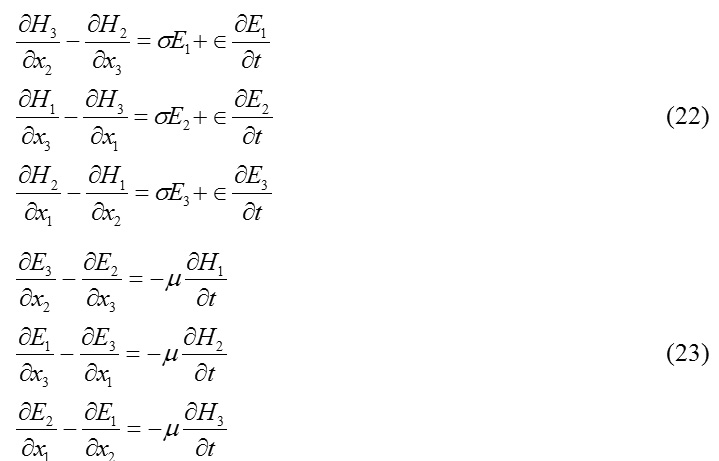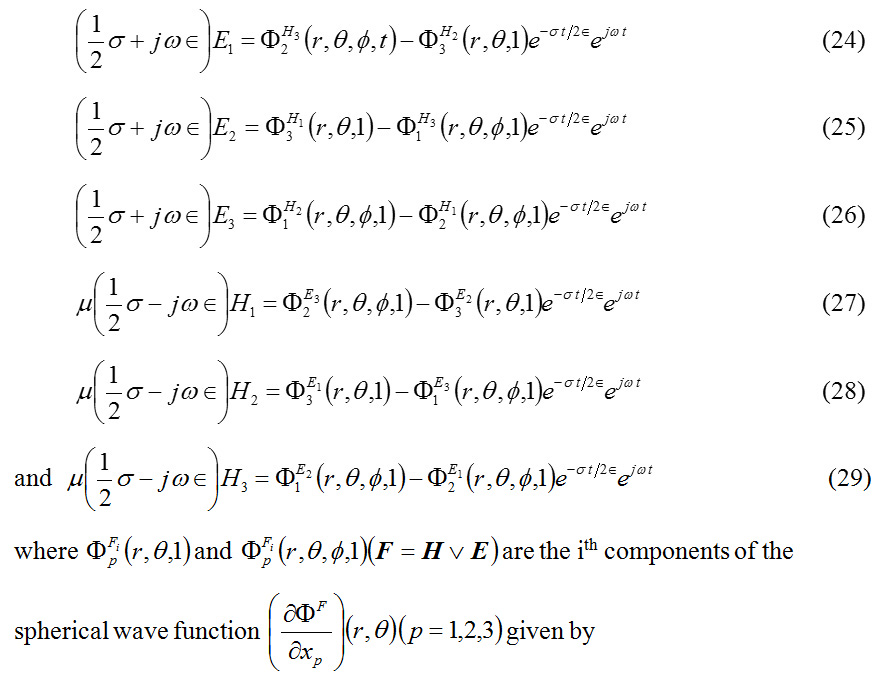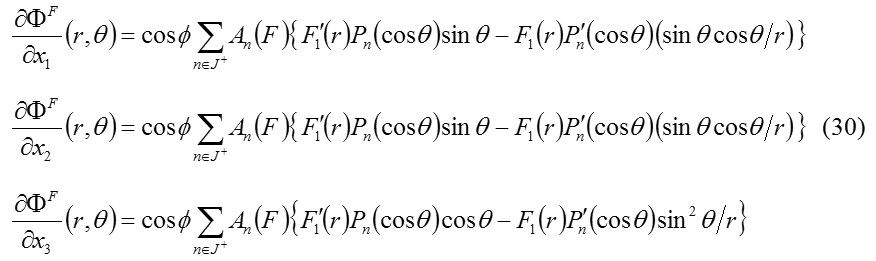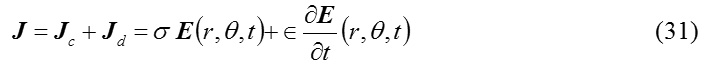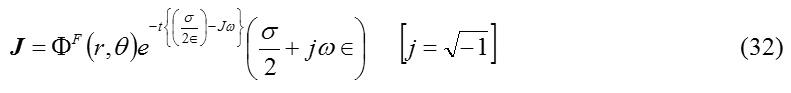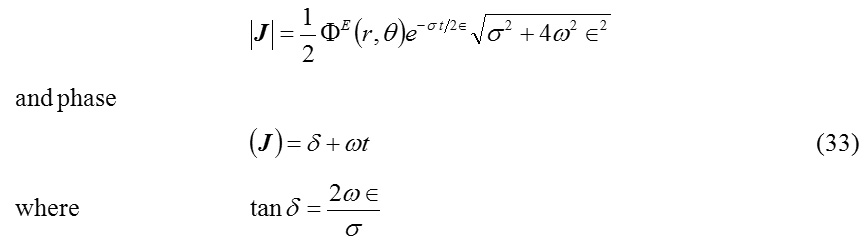Electromagnetic Wave Propagation through Triangular Antenna Subject to Longitudinal Symmetric Conditions
S. Kumar
P. G. Centre Department of Mathematics, Ram Dayalu Singh College, Muzaffarpur-842002, Bihar, India
Article Publishing History
Article Received on : 20 Mar 2013
Article Accepted on : 07 May 2013
Article Published : 06 Jan 2014
Plagiarism Check: Yes
Article Metrics
ABSTRACT:
Electromagnetic (EM) field intensities happen to exist as solutions of Maxwell’s equations in a three dimensional space. In the present paper an attempt has been made to determine the components of EM field intensities belonging to a pair of groove regions adjacent to a convex triangular prism. Field intensities are supposed to be longitudinal symmetry and the triangular prism forms a part of an echellete grating of fixed period. Two existence theorem regarding longitudinal symmetric electric intensity vector and magnetic intensity vector associated with time dependent spherical wave have been established. Finally, the expression for the current density associated with the prism has been derived.
KEYWORDS:
Electromagnetic field intensities;Convex triangular prism; Maxwell’s equations
Copy the following to cite this article:
Kumar S. Electromagnetic Wave Propagation through Triangular Antenna Subject to Longitudinal Symmetric Conditions. Mat.Sci.Res.India;10(2)
|
Copy the following to cite this URL:
Kumar S. Effect of Tin Additions on Microstructure and Mechanical Properties of Sand Casting of AZ92 Magnesium Base Alloy. Mat.Sci.Res.India;10(2). Available from: http://www.materialsciencejournal.org/?p=105
|
INTRODUCTION
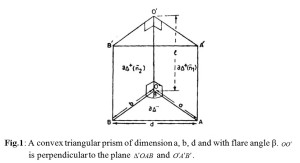
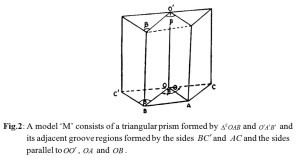
A convex triangular obstacle forms a vital part of a periodic echellete grating. In recent years1-10 quite a good number of results have been reported pertaining to the reflection, grazing and the diffraction of a propagating EM wave through a smooth, conducting and convex triangular obstacle K (Fig. 1). The obstacle is supposed to be hollow with an open rectangular base having the flare angle β, the groove depth ‘h’ and the period ‘d’ associated with the said echellete grating. In the present paper a model M (Fig. 2), consisting of a convex triangular obstacle and its adjacent wedge regions Ri (i = 1, 2), has been considered for interacting with a propagating EM wave. EM field intensities are generated due to propagating EM wave subject to governing Maxwell’s equations
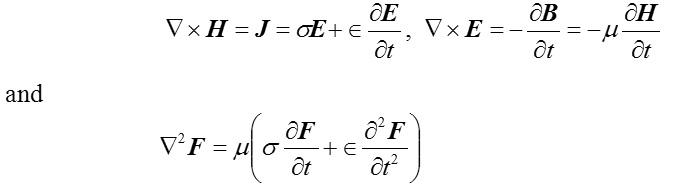
where H , E and F=(H v E) being magnetic intensity vector, electric intensity vector and their combination respectively. The physical elements σ,Î, m, J and B stand for conductivity, permittivity, permeability, current density and magnetic flux density associated with the model. The object of present paper is to determine the vector field intensity F by using spherical polar coordinates (r, θ, f) subject to the assumption ∂F / ∂ø = 0 (Longitudinal symmetric condition), leading finally to a spherical wave. Two existence theorems have been established for finding the components of H and E is associated with the Maxwell’s equations in H and E justifying thereby the transmission (σ ≠ 0) of the concerning EM waves through K. The result has been further utilized for computing the current density J.
FORMULATION OF THE PROBLEM
Consider the Maxwell’s equation
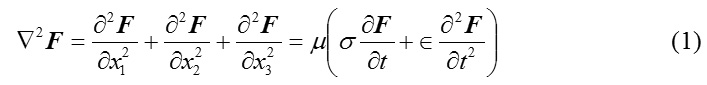
where F=F(x1,x2,x3,t) stands for vector field intensity. Transforming (1) by using spherical polar coordinates x1=r sin θcos Φ , x2=r cos θ sin Φ , x3=r cos θ one can arrive at the equation
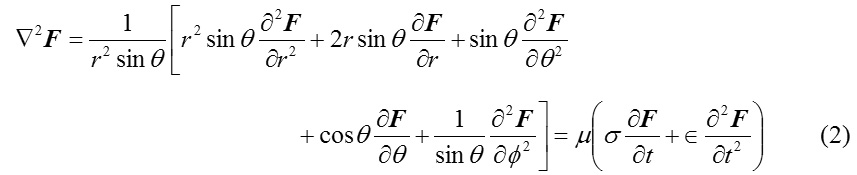
Now, using the variable separable method, one can arrive at the solution of the equation (2) in the form
and
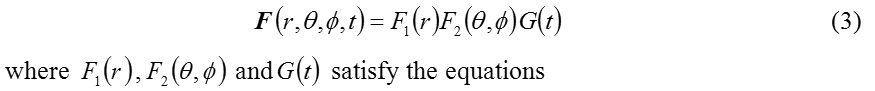
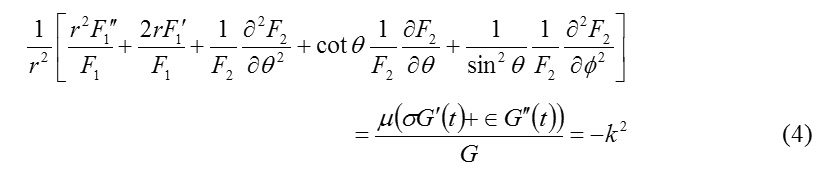
and
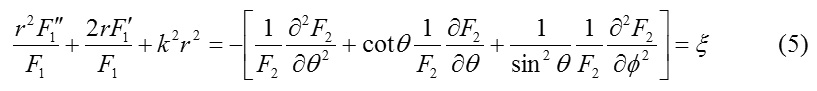
where the constants k and x are independent of r, θ, Φ and t.
In particular, assuming then equation (5) give arise to the surface harmonic function F2(θ,Φ) satisfying the equation
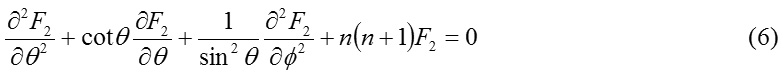
Again, separating ‘F2’ further in the form of the product

one can arrive at the equations

and
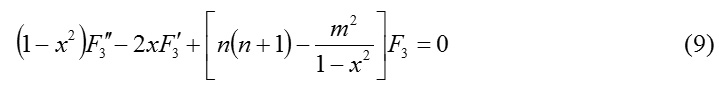
where x=cos θ, m is independent of θ.
The equation (9) may be identified as associated Legendre’s equation which furnishes the associated Legendre’s function as one of its solutions. Thus, combining (7), (8) and (9), the surface harmonic function F2(θ, f) may be expressed in the form
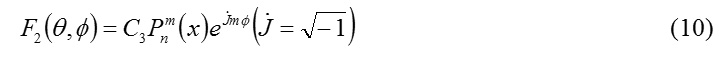
where C3 is an arbitrary constant.
Now, introducing longitudinal symmetry condition ∂F / ∂ø = 0 for the EM field F(r, θ, f, t) the equation (9) apparently reduces to the Legendre’s equation
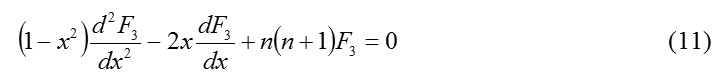
furnishing thereby the Legendre polynomial Pn(x) as one of its solutions, and consequently the solution (10) reduces to the form

Now, recalling the equation (5) again, one can arrive at the ordinary differential equation
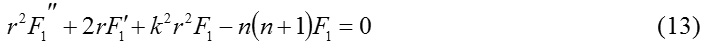
which possesses the only regular singular point at r = 0 and as such applying Frobenius method one can arrive at the series solution of (13) in the form
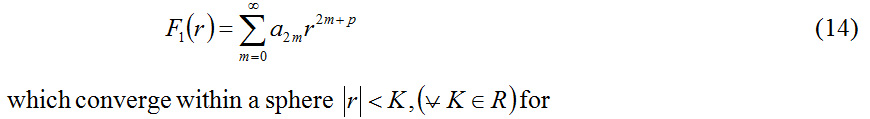

and the coefficients a2m satisfy the recurrence relation
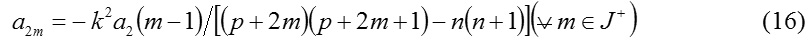
Again, referring to the equation (4), one can arrive at the equation

which furnishes the solution

where ‘A’ is an arbitrary constant,J√-1 , and
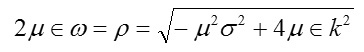
and k is the wave number restricted by the inequality

Hence, combining (3), (12), (16) and (18) one can arrive at the solution
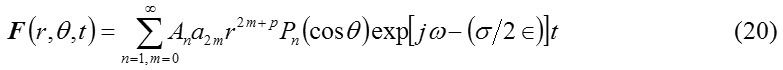
Spherical wave function and the components of electric and magnetic intensities vectors :
The expression (20) represent a spherical wave function

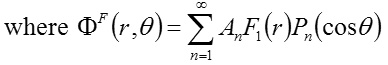
stands for the free space spherical wave formed by superimposition of spherical waves of amplitudes An(F). The natures of these waves are similar to that given by (20)
Now, recalling the Maxwell’s equations
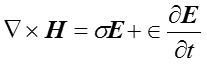
and
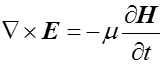
one can arrive at the following relations :
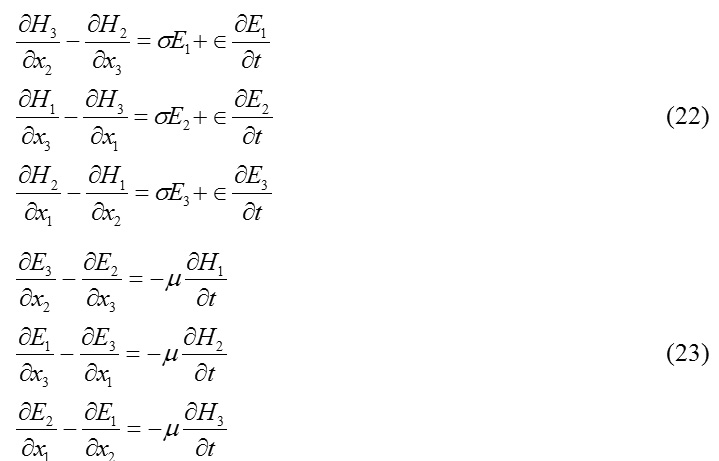
Replacing F by H, and E successively in (21) one can recast (22) and (23) in the forms :
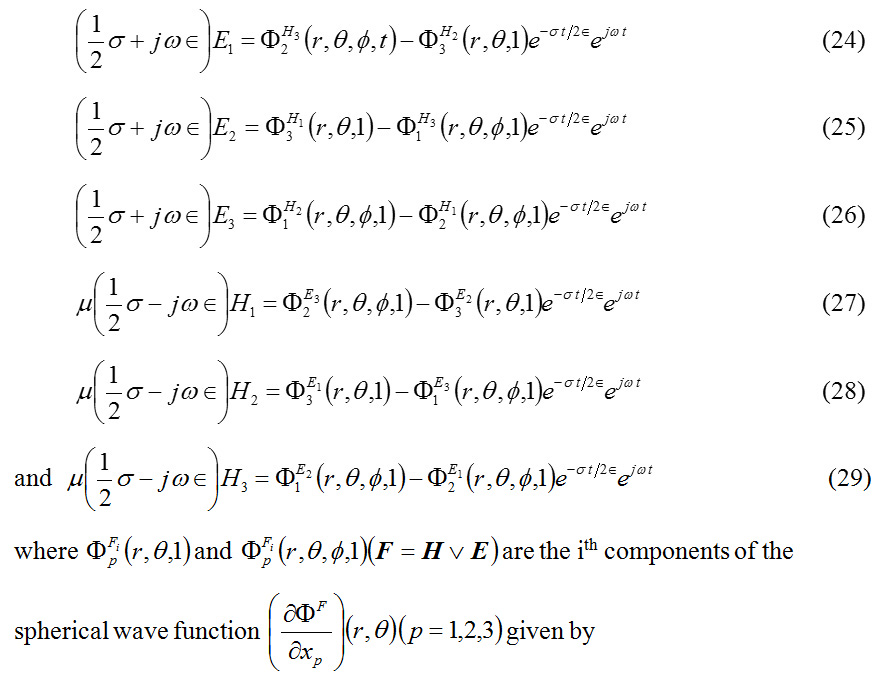
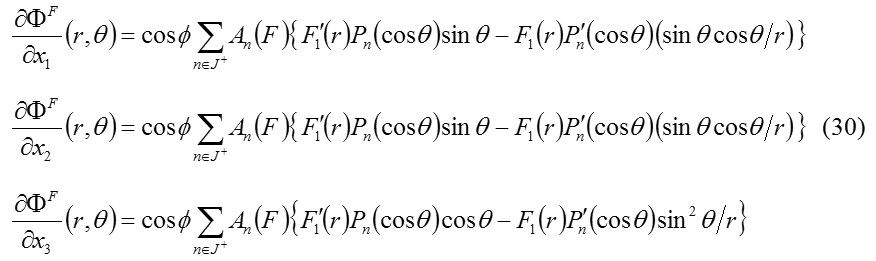
Hence, one can arrive at the following theorems :
Theorem-1
A longitudinally symmetric electric intensity vector is said to be associated with time dependent damped spherical wave ΦH(r,θ,t) of frequency ω with the damping factor (σ/2 ε) if the bounding surfaces of ∂K are conducting (σ≠0 ) and the components of magnetic intensity vector E are given by (27) to (29) and the frequency ω and the wave number k are mutually related as 4εk2 = μ(4 ε ω2 +σ2) subject to the restriction 2k√ ε > √ μ σ.
Determination of current density
A current density J consists of displacement current and the conduction current according to Maxwell’s theory in electromagnetics11.
Hence, one can express J in the form
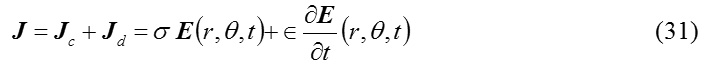
Now, combining the relations (21) and (31), J may be finally expressed in the following form
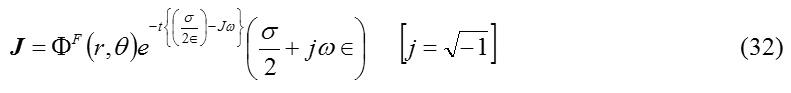
which represents a spherical wave with its modulus and the phase given by the following expressions
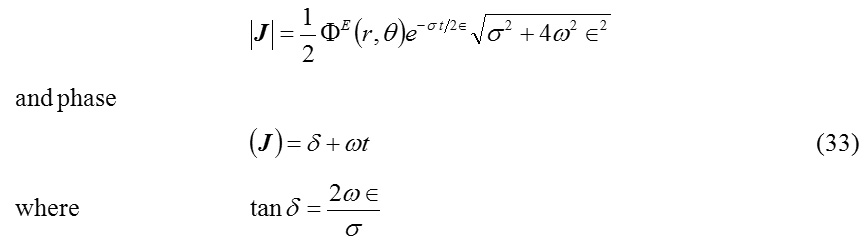
CONCLUSIONS
The present paper furnishes the existence of longitudinally symmetric EM waves. Such waves may be designated as longitudinally symmetric spherical waves. The concerning wave functions have been determined as solutions of the governing Maxwell’s equations in spherical coordinates . The governing Maxwell’s equations have been encountered for finding the magnetic field intensity and electric field intensity vectors. Finally the result has been used for computing the current density.
ACKNOWLEDGEMENTS
Thanks are due to UGC Minor Research Project for financial support [Grant no. PSB-004/11-12 dated 3 August-2011]
REFERENCES
- Bhowmick K. N. and Dey K. K., J. Electronics and Telecom Engineers 30: 112 (1984).
- Bhowmick K. N., J. Electronics and Telecom Engineers 34: 319 (1988).
- Bhowmick K. N. and Kumar Sanjay, Indian J. Phys. 65 B (4): 329 (1991).
- Kumar Sanjay, Prog. of Maths. 27 (1&2): 55 (1993).
- Kumar Sanjay, Proc. Math. Soc. B.H.U.11: 59 (1995).
- Kumar Sanjay, Proc. Math. Soc. B.H.U. 24: 29 (2008).
- Kumar Sanjay, Proc. Math. Soc. B.H.U. 26: 35 (2010).
- Kumar Krishan and Kaur Sukhdeep, International Journal of Scientific & Engineering Research 2: 1(2011).
- Wei K. P., Zhang Z. J. and Freng Z. H., Progress in Electromagnetic Research 126:101 (2012).
CrossRef
- Lee Hong-Min and Choi Wong-Sang, Wireless Engineering and Technology 4:5 (2013).
- C. R. Wylie, Advanced Engineering Mathematics, International Student edition Macgraw Hill Book Company Inc. (second edition): 520 (1960).

This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal