An Elastic Moduli Independent Approximation to the Radius of Curvature of the Bimetallic Strip
Amol Madhav Khatkhate  , R. Mannoj Paul Singh* and P. T Mirchandani
, R. Mannoj Paul Singh* and P. T Mirchandani
Dept. of. Mechanical Engineering, Rizvi College of Engineering, Mumbai, India, 400050.
Corresponding author Email: amol.khatkhate@gmail.com
DOI : http://dx.doi.org/10.13005/msri/140111
Article Publishing History
Article Received on : 21 June 2017
Article Accepted on : 30 June 2017
Article Published : 30 Jun 2017
Plagiarism Check: Yes
Article Metrics
ABSTRACT:
A parametric approach has been used to derive an approximate formula for the prediction of the radius of curvature of a thin bimetallic strip that at initial ambient temperature, is both flat and straight, but at above ambient temperature, forms into an arc of a circle. The formula enables the evaluation of the radius of curvature of the strip as a function of heating or cooling. A formula for calculating the radius of curvature of a bimetallic strip already exists, and was produced by Timoshenko in his paper on Bimetallic Thermostats. The formula by Timoshenko has been vigorously tested, tried and proven and accepted in countless papers and journals since its original publication. The parametric approach solution introduced in this work gives an approximate solution to the Timoshenko formula for equal thicknesses of two mating metals within the bimetallic. The Khatkhate Singh Mirchandani (KSM) formula presented here is taken from the first order approximation derived by Angel and Haritos by incorporating the ratio of Young's modulus of the bimetallic materials. Furthermore, researchers in this area have proven that the Young's modulus does not have a significant effect on the radius of curvature. Taking this fact into consideration, the authors have suitably incorporated a correction modifier purely based on the coefficient of thermal expansion (CTE) of the materials. The simulation results and the overall close agreement with the Timoshenko formula has been put forward here. Also, the solution derived by the authors Khatkhate et.al shows better prediction as compared to the solutions derived by other researchers.
KEYWORDS:
Bimetallic strip; INVAR 36; Low coefficient of expansion (CTE); Timoshenko
Copy the following to cite this article:
Khatkhate A. M, Singh R. M. P, Mirchandani P. T. An Elastic Moduli Independent Approximation to the Radius of Curvature of the Bimetallic Strip. Mat.Sci.Res.India;14(1)
|
Copy the following to cite this URL:
Khatkhate A. M, Singh R. M. P, Mirchandani P. T. An Elastic Moduli Independent Approximation to the Radius of Curvature of the Bimetallic Strip. Mat.Sci.Res.India;14(1). Available from: http://www.materialsciencejournal.org/?p=5712
|
Introduction
The original Timoshenko1 bimetallic bending formula was published in 1925 and since then has been extensively applied by multitudes of engineers and scientists and referred to in many papers such as by Krulevitch,2 Prasad3 and books Kanthal,4 Whilst it has been proven and accepted to be the formula to evaluate the hot radius of curvature of an initially flat bimetallic strip, it is an unwieldy and a complex formula to evaluate. This work introduces a new simpler, quicker method to evaluate the radius of curvature of the bimetallic strip from an initially flat ambient condition that has been uniformly heated. When a bimetallic strip is uniformly heated along its entire length, it will bend or deform into an arc of a circle with the radius of curvature, the value of which, is dependent on the geometry and metal components making up the strip. Also, the nature of the bend is a function of temperature change from the ambient is characteristically asymptotic. The new formula, introduced here is taken from the first order approximation by Angel and Haritos with suitable incorporation of the ratio of Young’s modulus of elasticity of the two materials that form the bimetallic.
The new formula introduced here, closely approximates to the Timoshenko formula with the exception of accommodating the change in the thicknesses of the two mating metals making up the bimetallic strip. It is important to note that in the majority of applications of bimetallic strip, the ratio of the thickness of the two constitute metals is normally one to one, i.e. of equal thickness. This comes about due to the way that the bimetallic strip is manufactured. The dominant method in the mass production of commercially available bimetallic strip involves either hot or cold rolling the two separate metals under intense pressures to produce interstitial bonding of the atoms at the bi- material interface Uhlig.5 Under such conditions, it is expensive, because of setup costs, to make special separate metal thicknesses unless specifically required. Moreover, there is no data to support that different thicknesses of the bimetals in the strip would have any performance benefit over equal thickness bimetal strip.
Cladding of metals Haga6 is used to provide a product with a less expensive base metal that benefit from a thinner skin for decorative and or surface protection purposes, although clad metals are technically bimetallic metals, clad bimetallic strip is not being used for its functional bending qualities. Therefore the need to cater for separate material thicknesses is not required for most applications where the bimetallic bending qualities of a bimetallic strip are being exploited.
Derivation of the Khatkhate Singh Mirchandani (KSM) model :
A. Timoshenko formula
From the Timoshenko [1], the radius of curvature of a bimetallic strip is given by:
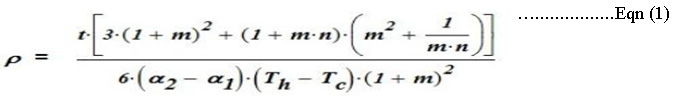
Where ρ is the radius of curvature, t, total thickness of the strip, t1 and t2 are the individual material thicknesses.
m = t1/t2 is the ratio of thicknesses.
n = E1/E2 is the ratio of the Young’s Moduli.
Th and Tc are the hot and cold temperatures states.
E2, E1, is the linear modulus of the two materials.
α1 & α2 are the coefficients of linear thermal expansion for the two metals.
α2 is assumed to be numerically larger than α1
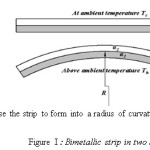
Figure I shows a bimetallic strip in two states of heating, at state 1, at ambient temperature, the strip will be flat with
no discernible radius of curvature R. At state 2, uniformly distributed
Figure 1 : Bimetallic strip in two states of heating
Note that has a numerically higher coefficient of linear thermal expansion and thus naturally wants to extend further than the side with The differences, leads to internal stresses, forces and moments at the material interface, resulting in the bending as shown at state 2.
B. Approximation model by correction factors (Angel and Haritos)
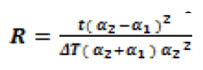
where the correction factor is denoted by β = (α2 – α1)2/(α2 + α1)α22 Referring to the paper by Angel and Haritos [8], further modification to the first order estimate is done by considering some modifiers and correction factors. For details, kindly refer,8 and the model is put here for completeness of the paper.
C. Khatkhate Singh Mirchandani (KSM) model
The authors of the paper have derived the model based on the first order approximation to the Timoshenko formula. Actually, the first order approximation does not incorporate the Young’s moduli of the two materials. However, the following equation
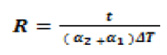
Where:
R is the radius of curvature of the bimetallic strip to the bimetallic joint center line (m).
t is the total thickness of the bimetallic strip(m).
k = constant depending on the base material.
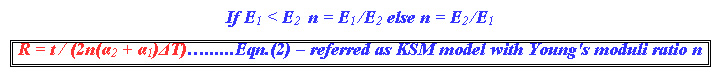
Where:
R is the radius of curvature of the bimetallic strip to the bimetallic joint center line (mm).
t is the total thickness of the bimetallic strip(mm).
As seen in Eqn.2, by introducing a suitable function of the Young’s moduli in the Khatkhate et. al model, the approximation is fairly improved as compared to other models by Angel and Haritos.8 Furthermore, it can be seen that the radius of curvature of the approximate curve R (from eqn.6), is slightly larger numerically, than the Timoshenko line. Thus a possible correction factor needs to multiply R by a number slightly less than unity. Introducing a proportional correction factor reduces the value of R to a very close approximation of Timoshenko ρ.
Thus letting λ = (α1/α2 )2 and η = 1 – λ, we can re-write the new approximation as follows:

It can be observed that the new approximation in Eqn. 3 is independent of the ratio of the Young’s moduli ‘n’ and also results in a lowering of R for most of the cases as seen in the simulation and results section. The constant k is a material constant that needs to be optimized for every new base material and we have optimised it for Invar 36 as sqrt(2).
Simulation Results and Discussion
The first simulation was based around a bespoke Bimetallic strip SBC206-1 from Shivalik7; 100mm long x 5mm wide x 0.4mm thick , these were the starting values of the first simulation set.
E2 = 213 GPa ; Young’s modulus of Steel side of the bimetallic strip.
E1 = 145 GPa ; Young’s modulus of Invar 36 side of the bimetallic strip.
α1 = 1.45e-06 m/m/°C ; coefficient of linear thermal expansion for Invar36 side of the strip.
α2 = 18.5e-06 m/m/°C ; coefficient of linear thermal expansion for Steel side of the strip.
t = t1 + t2, both equal, total thickness of the strip.
Tc = 20°C assumed ambient temperature constant throughout the simulation. Th = Input variable temperature (°C).
ΔT = change in temperature , (°C).
Figure 2: Comparison of performance of models for Shivalik[7] 0.4 mm thick bimetallic strip (assuming constant coefficient of expansion for Invar 36) with the Timoshenko formula
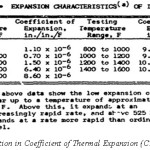
The Figure II above shows the performance of the various models to the Timoshenko formula. In-order to compare the same, mean square error is computed for all the approximations. As seen in Figure, the approximation by Khatkhate et al shows the least error almost 8-12 times less than the other models. The 2nd simulation was performed considering the effect of temperature on the coefficient of thermal expansion (CTE) of Invar 36 (See Table 1). As seen in Figure III, the error of the models increases as we consider the variation in coefficient of thermal expansion (CTE) of Invar 36. The KSM model fits well for high temperature range (greater than 180 degree C), however, the models by Angel and Haritos show lesser error with CTE variation which is evident as α1 becomes comparable to α2 .
Large chi-square or RMSE values (≥0.5 and 1.0, respectively) reflect the model’s poor ability to accurately predict the radius of curvature even the model is having large R2 value (≥0.7). For good predictive model the chi and RMSE values should be low (<0.5 and <0.3, respectively).10
Table 1 : Variation in Coefficient of Thermal Expansion (CTE) of Invar 36
Figure 3: Comparison of performance of models for Shivalik7 0.4 mm thick bimetallic strip (for varying CTE of Invar 36) with the Timoshenko formula.
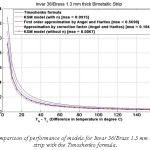
Figure 4: Comparison of performance of models for Invar 36/Brass 1.3 mm thick bimetallic strip with the Timoshenko formula
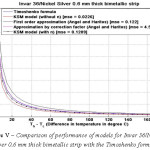
Figure 5: Comparison of performance of models for Invar 36/Nickel Silver 0.6 mm thick bimetallic strip with the Timoshenko formula
Figure 6: Comparison of performance of models for Invar 36/Mild Steel 1.6 mm thick bimetallic strip with the Timoshenko formula
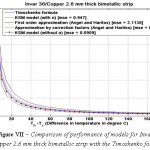
Figure 7: Comparison of performance of models for Invar 36/Copper 2.6 mm thick bimetallic strip with the Timoshenko formula.
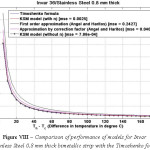
Figure 8: Comparison of performance of models for Invar 36/Stainless Steel 0.8 mm thick bimetallic strip with the Timoshenko formula
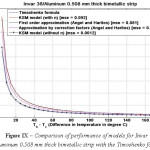
Figure 9: Comparison of performance of models for Invar 36/Aluminum 0.508 mm thick bimetallic strip with the Timoshenko formula.
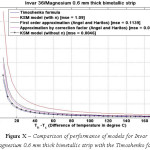
Figure 10: Comparison of performance of models for Invar 36/Magnesium 0.6 mm thick bimetallic strip with the Timoshenko formula.
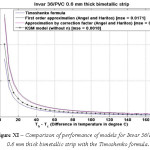
Figure 11: Comparison of performance of models for Invar 36/PVC 0.6 mm thick bimetallic strip with the Timoshenko formula
Simulation Set 3
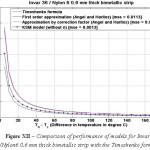
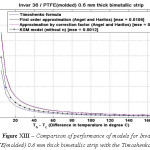
The various models were simulated with different materials in combination with Invar 36 as the base material in-order to test the robustness of the formula. Please refer Figure IV-XIII for the performance of the various models with different bimetals. The errors were tabulated in Table 2. As seen, the Khatkhate Singh Mirchandani (KSM) model without Young’s moduli ratio (n) performed best with very low rmse below 0.3 in 9 out of 10 randomized cases.
Table 2: Simulation set 3 of Invar 36 with various other materials
|
|
|
|
|
|
Ref
|
|
KSM
(w/o n)
|
First Order (A & H)
|
Correction Factor (A & H)
|
KSM (with n)
|
|
Invar 36 / Brass
|
0.65
|
1.45
|
141
|
0.08
|
0.75
|
0.32
|
0.3
|
12
|
|
0.65
|
18.7
|
111
|
15
|
|
Invar 36 / Nickel Silver
|
0.3
|
1.45
|
141
|
0.15
|
0.35
|
0.02
|
0.36
|
12
|
|
0.3
|
13
|
118
|
14
|
|
Invar 36 / Mild Steel
|
0.8
|
1.45
|
141
|
0.51
|
1.02
|
0.32
|
0.66
|
12
|
|
0.8
|
11
|
195
|
16
|
|
Invar 36 / Copper
|
1.3
|
1.45
|
141
|
0.3
|
1.45
|
0.43
|
0.97
|
12
|
|
1.3
|
16.6
|
117
|
17
|
|
Invar 36/ Stainless Steel
|
0.4
|
1.45
|
141
|
0.03
|
0.5
|
0.2
|
0.05
|
12
|
|
0.4
|
17.3
|
213
|
18
|
|
Invar 36 / Aluminum
|
0.25
|
1.45
|
141
|
0.04
|
0.28
|
0.18
|
0.3
|
12
|
|
0.25
|
23.5
|
69
|
13
|
|
Invar 36 / Magnesium
|
0.3
|
1.45
|
141
|
0.07
|
0.34
|
0.24
|
1.04
|
12
|
|
0.3
|
26
|
40
|
19
|
|
Invar 36 / PVC
|
0.25
|
1.45
|
141
|
0.04
|
0.13
|
0.12
|
Large
|
12
|
|
0.25
|
70
|
3
|
19
|
|
Invar 36 / Nylon 6
|
0.3
|
1.45
|
141
|
0.04
|
0.11
|
0.1
|
Large
|
12
|
|
0.3
|
87.3
|
2.2
|
19
|
|
Invar 36 / PTFE (molded)
|
0.3
|
1.45
|
141
|
0.03
|
0.1
|
0.09
|
Large
|
12
|
|
0.3
|
107
|
0.56
|
19
|
Figure 12: Comparison of performance of models for Invar 36/Nylon6 0.6 mm thick bimetallic strip with the Timoshenko formula
Figure 13: Comparison of performance of models for Invar 36/PTFE(molded) 0.6 mm thick bimetallic strip with the Timoshenko formula
Acknowledgements
The authors would like to express deepest appreciation towards Dr. Varsha Shah, Principal RCOE, Mumbai and Prof. Husain Jasdanwala whose invaluable guidance in this research project has brought it to this stage. Also, the first author would like to thank Professor Mirchandani for encouragement to teach the subject of Mechanical Measurements and Controls (MMC) which helped him in reading more about the work done by Timoshenko and other researchers on the Bimetallic Thermostats. At last the authors express their sincere heartfelt gratitude to all the staff members of Mechanical Engineering Department who helped us directly or indirectly during this course of work.
References
- Timoshenko S. Analysis of Bi-metal Thermostats. JOSA. 1925;11(3):233-255.
CrossRef
- Krulevitch P., J. G. C. Curvature of a Cantilever Beam Subjected to an Equi-Biaxial Bending Moment. in Materials Research Society Conference. 1998.
- Prasad K. Principle and Properties of Thermostat. Journal of Materials. 1993.
- Kanthal, Kanthal Thermostatic Bimetal Handbook., Box 502, SE-734 27 Hallstahammar Sweden: Kanthal. 2008;130.
- Uhlig W., et al. Thermostatic Metal, Manufacture and Application. 2nd, revised ed. 2007, Hammerplatz 1, D-08280,Aue/Sachsen: Auerhammer Metallwerk GMBH. 198.
- Haga T. Clad strip casting by a twin roll caster. World Academy of Materials and Manufacturing Engineering. 2009;37(2):117-124.
- Shivalik S. Bimetallic strip supplier. 2013; Available from: http://www.shivalikbimetals.com. Accessed online Sept. 2013.
- Angel G. D., Haritos G. An immediate formula for the radius of curvature of the bimetallic strip. International Journal of Engineering Research & Technology (IJERT). 2013;2(12).
- Khatkhate A. M., Paul M. R. S., Mirchandani P. T. A parametric approximation for the radius of curvature of the bimetallic strip. International Journal of Engineering Research & Technology (IJERT). 2017;6(6).
- Veerasamy R., Rajak H., Jain A., Sivadasan S., Varghese P. C and Agrawal K. R. Validation of QSAR models : Strategies and Importance. International Journal of Drug Design and Discovery. 2011;2(3):.511-519.
- McCain., William S. Mechanical and Physical properties of Invar and Invar type alloys. Batelle Memorial Institute, Columbus, Ohio. 1965;43.
- http://www.nickel-alloys.net/invar_nickel_iron_alloy.html Physical_properties, WWW accessed. 2013.
CrossRef
- http://www.smithmetal.com/downloads/1050A.pdf, WWW accessed. 2013.
CrossRef
- http://www.cuivre.org/contenu/docs/doc/pdf/CuNiZn/CuNi10Zn27.pdf, WWW accessed. 2013.
CrossRef
- http://www.copperinfo.co.uk/alloys/brass, WWW accessed. 2013.
CrossRef
- http://www.matweb.com/mild steel, WWW accessed. 2013.
CrossRef
- http://www.aalco.co.uk/datasheets/Copper~Brass~ Bronze_CW024A-C106_122.ashx, WWW accessed. 2013.
CrossRef
- Munday A. J and Farrar R. A An Engineering Data book , MacMillan, London.
- http://www.matweb.com WWW accessed. 2017.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.
 , R. Mannoj Paul Singh* and P. T Mirchandani
, R. Mannoj Paul Singh* and P. T Mirchandani Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal

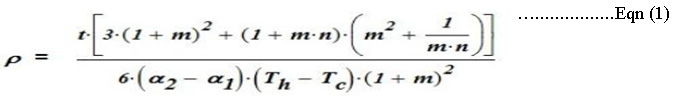
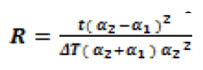
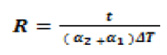
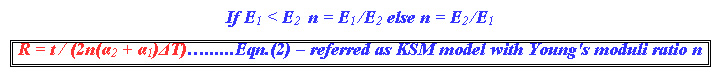

![Figure II – Comparison of performance of models for Shivalik[7] 0.4 mm thick bimetallic strip (assuming constant coefficient of expansion for Invar 36) with the Timoshenko formula](http://www.materialsciencejournal.org/wp-content/uploads/2017/06/Vol14_No1_ela_Amo_fig2-150x150.jpg)
![Figure III – Comparison of performance of models for Shivalik[7] 0.4 mm thick bimetallic strip (for varying CTE of Invar 36) with the Timoshenko formula.](http://www.materialsciencejournal.org/wp-content/uploads/2017/06/Vol14_No1_ela_Amo_fig3-150x150.jpg)