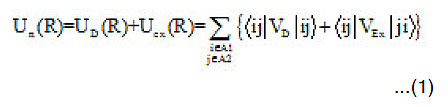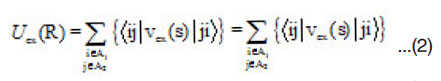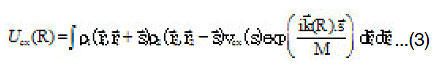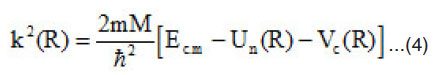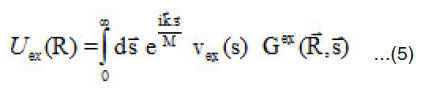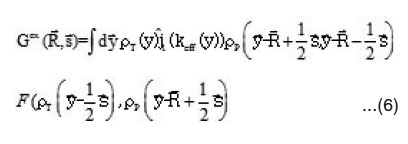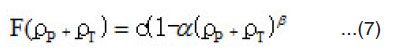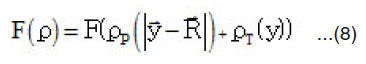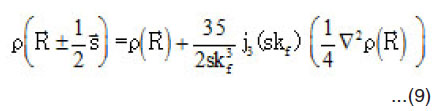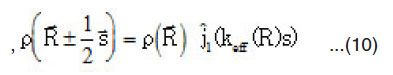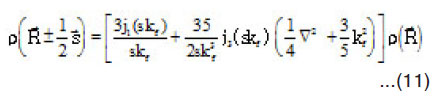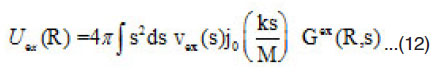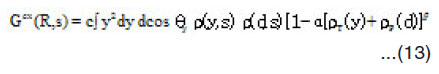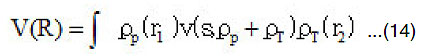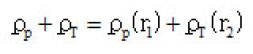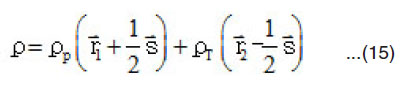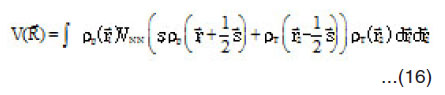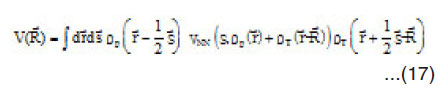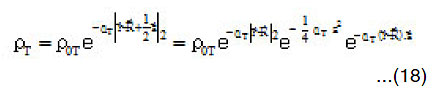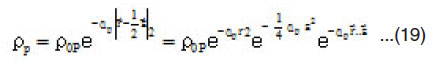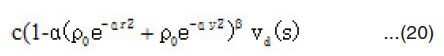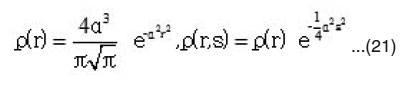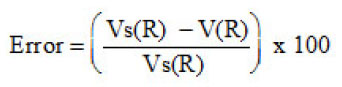Effect of Local Density Dependence on the Exchange and Direct Part of A-A Interaction Potential

M. Y. Ismail, H. Elgebaly* and M. M. Osman

Physics Department, Faculty of Science, Cairo University, Cairo, Egypt.

DOI : http://dx.doi.org/10.13005/msri/070102

ABSTRACT:

The study show that the error in neglecting s-dependence affects strongly both the values of U_ex and U_tot . This effect is about 30 %( 23%) in U_ex (U_tot) for the force BDM3Y2 -Reid type while it is less than 7% for BDM3Y1-Ried. It decreases as α– α separation distance increases. For BDM3Y3 type force the corresponding error is too large at separation distance R=0.

KEYWORDS: α– α interaction potential; Local density dependence

Copy the following to cite this article: Ismail M. Y, Elgebaly* H, Osman M. M. Effect of Local Density Dependence on the Exchange and Direct Part of A-A Interaction Potential. Mat.Sci.Res.India;7(1)

Copy the following to cite this URL: Ismail M. Y, Elgebaly* H, Osman M. M. Effect of Local Density Dependence on the Exchange and Direct Part of A-A Interaction Potential. Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2206

Introduction

The most famous models used for deriving the interaction potential are the two–center shell model,^1-3 the energy density formalism,^4-7 the proximity method⁸ and the double folding model.⁹ Recently, the double folding model was developed in two ways .The first is the calculation of its exchange part using finite range NN force. This development produces some computational difficulties if the non diagonal densities, appearing in this part, were not approximated using the density matrix expansion method of Negele and Vautherin.¹⁰ The other development is the use of realistic effective NN force which is usually density dependent.^11-16 Again density dependence of NN force produces difficulties in numerical calculations. To overcome this difficulty the nucleon–nucleon separation distance in the density dependent NN force is considered when calculating the direct HI potential part and is neglected for the exchange part. This approximation in considering the density dependence of NN interaction needs to be tested.

The Generalized Double Folding Model

The double-folding model^17-18 proved to be quite successful in obtaining the correct values of the real part of the optical model potential needed to fit elastic scattering data. In this model the real potential U_n(R) is the sum of the direct part U_D(R) and the exchange part U_ex(R). Earlier studies led to the calculation of the real potential on the assumption that the exchange part of the nucleon-nucleon interaction is a zero range.^19-20 Such approximation produces correct ion-ion potential in the tail region only. 

The inner and surface regions can not be calculated with good accuracy using δ -force assumption. However, it is well established now that in certain cases of nuclear scattering observed first in α-particle²¹ and later for other light HI systems,^22-24 where the data are sensitive to the HI optical potential over a wider radial domain, the simple double folding model^17-18 failed to give a good description to the data. Therefore, some further developments of the folding model have been made to obtain a more realistic shape of the folding potential. One of these approaches is to impose on the widely used M3Y-NN interaction²⁵ explicit density dependence, the DDM3Y1 interaction.²⁶ Another is to treat correctly the simple Knock out effect arising from the Pauli principle. In the later approach the exchange part of the real HI optical potential is derived from the first principle instead of using a zero-range pseudo potential^27-31 adopted in the calculation with M3Y and DDM3Y1 interactions.^5,26,32 In ref. ^11-16,33 a simple microscopic approach has been developed based on generalization of the double folding and the density matrix.^34-35 In the framework of this model, the real part of the HI optical potential at a separation distance R between the centers of two ions is obtained by:

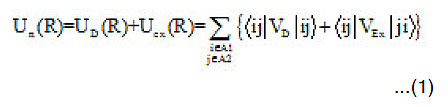
where |i> and |j> refer to the single-particle wave functions of nucleons in the two colliding nuclei A₁ and A₂ , respectively_; V_D and V_Ex are the direct and exchange parts of the effective NN interaction.

In this work we calculate the full ion-ion potential, U_n(R) =U_D(R)+U_ex(R) , for α–α nuclear pairs in the frame work of the generalized double folding model^14,25 using the effective BDM3Y^{14-16,25,36-37} nucleon-nucleon force. This work is show the accuracy of neglecting the S-dependence in the density-dependent NN interaction on both the direct and exchange parts of α–α interaction potential.

Calculation of the Exchange and Direct HI Potential Using Density Dependent NN Forces

In general, the exchange part of the real heavy ion potential must be non-local.³⁵ Since the exact treatment of the non-local exchange term is too complicated and needs a lot of numerical calculations, one usually obtains the equivalent local potential by representing the relative-motion wave function of the two interacting nucleons as plane wave,³⁵ Under such an assumption, the exchange part of the HI potential^11-18 is represented by,

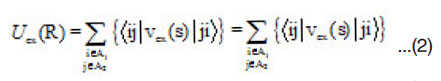
By introducing the one –body density matrix,^11-16 one can explicitly write equation (2) as:

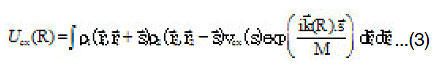
where k(R) is the relative–motion momentum given by [11-16]

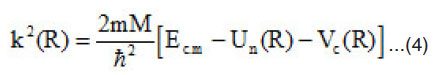
where M and E_c.m are the reduced mass, 

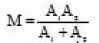
and relative energy in the center of mass system and m is the nucleon mass. Here U_n(R) and V_c(R) are total nuclear potential (U_n(R) = U_D(R)+ U_ex(R)), and coulomb potential, respectively. For density dependent NN force equitation (3) can be written as,

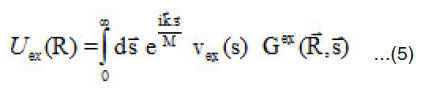
where G_ex (R, s)r  is given by [12,38]

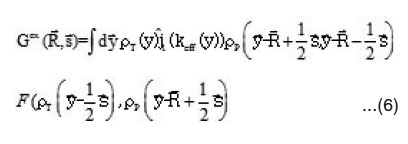
where density matrix expansion was used to simplify the non-diagonal density of the target nucleus. In most calculations [11-16] the s-dependence in the function F is neglected. In this case the direct and exchange parts of HI potential are not computed in consistent way regarding to the variables of density dependence in NN force. The function F has the following expression for BDM3Yn (n=1,2,3) type of forces

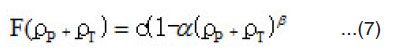
β have the values =1,2 and 3. The projectile non-diagonal density matrix can be expanded using DME³⁹ or it can be calculated exactly using oscillator model if the projectile is double closed shell light nucleus (as O¹⁶ and He⁴ )[34]. If one neglects the s-dependence in ρ appearing in the function F, it becomes

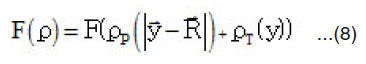
In general Gex depends on both the magnitude and direction of ex U (R). In this case, it is very difficult to calculate. So, we should use approximate methods to take into account the s-dependence in density dependent part of NN force. We use the approximations [40-42 respectively],

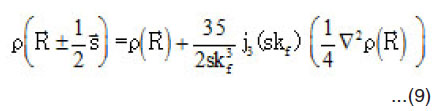
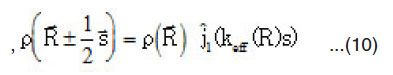
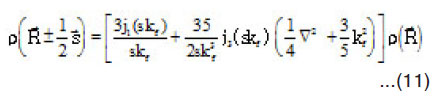
Taking in Z-direction and integrating over the variable, to get,

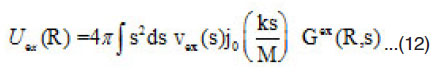
where ex G R,s) is given by [16,38]

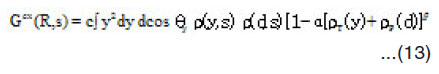
where 

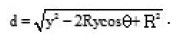
Since the nucleon relative momentum depends on the total real potential (equation (5)), the calculation of Uex need UD as input.

The direct part of α-α  potential is given by,

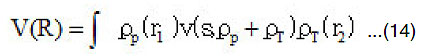
where

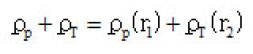
This shape of density dependence is used usually in the calculation of the direct part of the HI-potential, where the ρ-dependence of the NN potential is evaluated at the two positions of the interacting nucleons. This procedure is not consisting with that used in calculating the exchange part of the potential. For this part the density in the NN  exchange force is evaluated at the mid point separating the two nucleons. This means in the NN force is taken as:

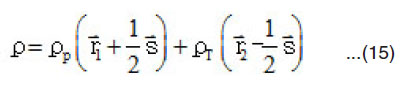
The aim of the present part is to estimate the effect of the difference between the two approaches on the direct α-α potential.⁴² The method of calculating the direct part using NN force depends on the density given by equation (14) is well known. It depends on taking the Fourier transform of the NN potential which depends on s. This reduces the six-dimensional integral of HI direct potential to integration over one-dimensional integrals. On the other hand equation (15) for the density dependence produces difficulties in calculating, the direct part of HI potential .In this case,

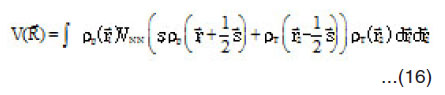
This can be simplified by changing the integration variables to get,

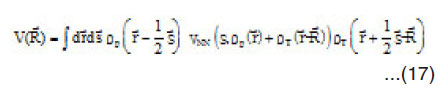
Equation (17) can be calculated when one assumes similar target and projectile nuclei with Gaussian shapes for densities. Taking Gaussian forms for the density distributions of both target and projectile

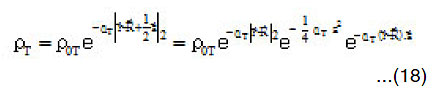
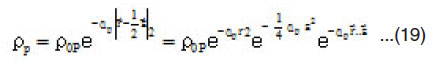
Substituting equations (18) and (19) into equation (17) and using the spherical harmonics basis then integrating over the solid angle of 

For similar projectile and target nuclei ( ), the last expression is simplified to

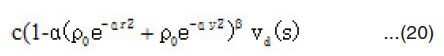
Where

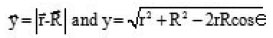
This expression can be easily calculated numerically.

Results and Discussion

For Exchange Part

Since the exact treatment of s-dependence in calculating nucleus-nucleus is too difficult. We use the approximations in equations (9-11). For α-particle,

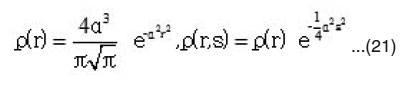
where b 1α = and b is the oscillator parameter and it has the value b= (1.33) fm.

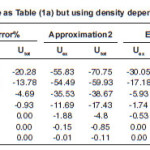
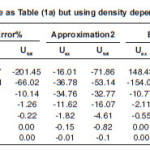
The effect of taking s-dependence in density appearing in NN force is to produce more attractive α -α interaction potential at small separation distances. The tables show that the error in neglicting s-dependence affects strongly both the values of U_ex and U_tot.

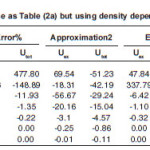
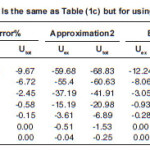
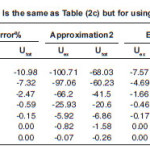
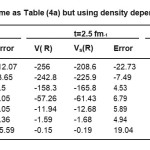
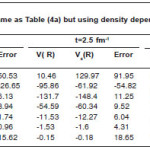
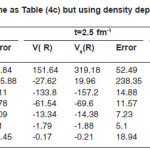
Table (1) contains the results for the separation distance variation of the α-α interacting pair calculated using BDM3Yn (n=1,2,3)- Reid force. Table (2) is the same as Table (1) expect Paris version of NN force was used. Part (a), (b) and (c) denote calculations using BDM3Yn with n=1,2 and 3 respectively. Both the tables were calculated for projectile energy per nucleon E_L/A_P= 5.2 MeV/N. The first column of each table shows the value of the nucleus-nucleus separation distance (R), the second column shows both Uex and U_D+Uex ( denoted by U_tot) . The second column was calculated using harmonic oscillator wave function to construct the diagonal and non diagonal densities. The third, forth and fiftieth column are our calculations by using the three approximations. The error on the tables are calculated as

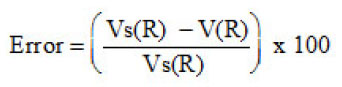
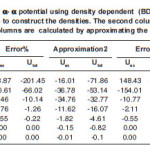
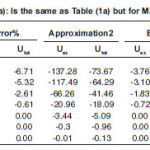
Tables (1) and (2) show the results of α-α calculated using a value b=1.33. The tables show that the effect of neglecting s-dependence increasesas the NN force becomes corresponding to higher value of incompressibility coefficient. This effect is about 30%(23%) in U ex (Utot) for the force BDM3Y2- Reid type while it is less than 7% for BDM3Y1-Ried. It decreases as the α–α separation distance increases. For BDM3Y3 type of force which corresponds to large value of compressibility coefficient, the corresponding error is too large at separation distance R=0, as Tables (1c) and (2c) indicate .This error becomes reasonable as the separation distance between the two α particles increases. The huge error obtained is due to the small radius of α–particle (about 1.58 fm.) and its large central density. Since the force BDM3Y3 corresponds to nuclear matter saturation curve in which E/A varies strongly when ρ becomes greater than the saturation density P0≅(0.17fm^-3), we expect large change in potential when the density changes slightly .In other words the force BDM3Y₃ is too sensitive to the value of ρ when the latter has value more than 0.17 fm-3 . In order to decrease this error, á –particle is artifficially made less localised. For this purpose we increased by about 13% to becomes (1.83 fm.) which corresponds to b=1.5 fm. Tables (3a) and (3b) are the same as (1c) and (2c) respectively except they are calculated using b=1.5fm. These tables show that when the α–particle becomes less localised, the error becomes reasonable.

Table 1a: Calculation of the exchange and total α- α potential using density dependent (BDM3Y1-Reid) NN interaction. Harmonic oscillator wave functions used in the calculations to construct the densities.

Click on image to enlarge

 Table 1(b): Is the same as Table (1a) but using density dependent ( BDM3Y₂) force

Click on image to enlarge

Table 1(c): Is the same as Table (1a) but using density dependent ( BDM3Y₃) force

Click on image to enlarge

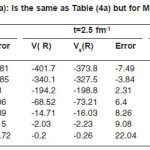
Table 2(a): Is the same as Table (1a) but for M3Y Paris

Click on image to enlarge

Table 2(b): Is the same as Table (2a) but using density dependent ( BDM3Y₂) force

Click on image to enlarge

Table 2(c): Is the same as Table (2a) but using density dependent (BDM3Y₃) force

Click on image to enlarge

 Table 3(a): Is the same as Table (1c) but for using b=1.5 fm

Click on image to enlarge

Table 3(b): Is the same as Table (2c) but for using b=1.5 fm

Click on image to enlarge

For Direct Part

In our study of the effect of local density dependence on the HI potential we consider interacting potential. The small mass number of α – particle produces large changes in the density distribution along the separation distance between the two centers of the interacting particles. This change in the density from point to point makes the effect of s-dependence in the density dependent part of NN force appears strongly for this system. For heavy nuclei, the value of the density distribution is nearly constant over a large distance measured from the center of the nucleus and the effect of s-dependence is small. To make this point more clearly we note that the density dependent contribution of the NN force contains the sum (ρ1 + ρ2). This term is calculated usually by assuming that the value of corresponds to the values of densities at the positions of the interacting nucleons (ρ1(r1) + ρ2(r2). Another way is to evaluate the sum of the two densities at a point midway between the interacting nucleons so that it is expressed as the sum. If the interacting nuclei have large mass numbers the two approaches produce almost the same value of the density and the effect of s-dependence becomes larger. For strong overlap between light nuclei there is a large chance that the total density 

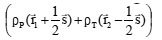
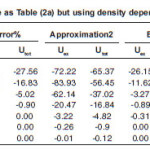
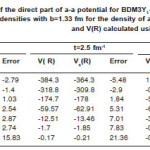
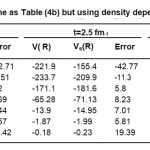
becomes larger than the same quantity after ignoring the s-dependence in the brackets of densities. Since the NN interaction is of the form, v(s,ρ) = cv(s)(1- αρβ), the appearance of s in ρ produces a NN interaction potential value small compared to the case when s-dependence is ignored. So, we expect that the HI potential calculated, for small R-values, using the form in NN force is enhanced compared to that calculated by including s r in the total density. This appears clearly for the NN force ranges 0.25 and 0.4 fm presented on tables (4) and (5) where the α – α potential V(R) and Vs(R) are calculated receptively using the expressions in the NN force density dependent term. Table (4) shows the potential calculated, at different separation distances R, using the BDM3Yn(n=1,2,3) -Reid NN forces. The table contains the contributions of V(R) and Vs(R) resulting from one Yukawa term with ranges 0.25 and 0.4 fm. and the same quantities calculated using NN force which contains the two ranges. Table (5) is the same as table (4) except it is for Paris type of force. The tables show that for one Yukawa is greater than, in most cases, for small R values. The error in neglecting the s-dependence increases as the range of NN force increases. This is reasonable for all separation distances between the two interacting nuclei. For, calculated using one Yukawa term in becomes smaller than. This is because as the separation distance between the two nuclei increases, the sum has large chance to be greater than during the integration process on the volume elements. This behavior is clear on tables (4) and (5), for the two separate Yukawa ranges 0.25 and 0.4 fm. When the two Yukawa terms are combined together to form M3Y-force, V(R) and Vs(R) becomes different in behavior than the case of single Yukawa term. For, V(R) is less repulsive or more attractive compared to V(R, s) .In the surface and tail regions V(R) becomes less attractive or more repulsive than Vs(R).

Table 4(a): Results of the direct part of a-a potential for BDM3Y1-Reid NN force using oscillator model densities with b=1.33 fm for the density of a particle. 

Click on image to enlarge

Table 4(b): Is the same as Table (4a) but using density dependent BDM3Y₂ force

Click on image to enlarge

 Table 4(c): Is the same as Table (4a) but using density dependent BDM3Y3 force

Click on image to enlarge

 Table 5(a): Is the same as Table (4a) but for M3Y Paris

Click on image to enlarge

Table 5(b): Is the same as Table (4b) but using density dependent BDM3Y₂ force

Click on image to enlarge

 Table 5(c): Is the same as Table (4c) but using density dependent BDM3Y3 force

Click on image to enlarge

For Reid type of NN force, the magnitude of the percentage error is too large in the inner region while it is smaller in the surface and tail regions. For Paris force the situation is different, the error in the total potential is too large at R=3fm.This large value of error is accompanied by small error values for the two Yukawa ranges 0.25 and 0.4 fm. This can be interpreted if we remember that the direct part of HI potential calculated using Paris NN force is repulsive at small R values then it passes through zero and becomes attractive. For the distance R=3 fm. the value of potential is too small and any small change between V(R) and Vs(R) produces large value of error. The difference between V(R) and Vs(R) together with the difference in HI potential due to change of NN force can be understood from Figs.(3) and (4) .

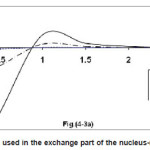
Figure 1: Coordinates used in the exchange part of the nucleus-nucleus interaction

Click on image to enlarge

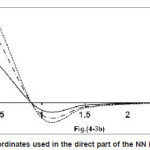
Figure 2: Coordinates used in the direct part of the NN interaction

Click on image to enlarge

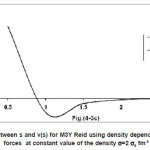
Figure 3(a): Relation between s and v(s) for M3Y Reid using density dependent BDM3Y_n(n=1,2,3) forces at constant value of the density σ=2 σ₀ fm^-3

Click on image to enlarge

Figure 3(b) Is the same as Fig.(3a) but at constant σ= σ0 fm-3

Click on image to enlarge

Figure 3(c) Is the same as Fig.(3a) but at constant σ= 0.5ñ₀ fm^-3

Click on image to enlarge

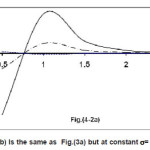
Figure 4(a) Is the same as Fig.(3a) but for M3Y Paris
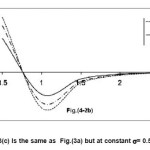
Figure 4(b) Is the same as Fig.(3b) but for M3Y Paris
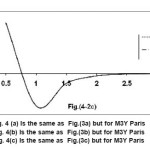
Figure 4(c) Is the same as Fig.(3c) but for M3Y Paris

Click on image to enlarge

Fig.(3) shows the variation of the direct part of Reid NN forces with the distance between the two interacting nucleons calculated at three different values of density. These values are, and where is the-particle density at the center of the nucleus. Fig.(4) is the same as Fig.(3) except it is for Paris interaction .It is noted that strong variation of NN force with internucleon distance produces large difference between V(R) and Vs(R). This is clear on table (4) for BDMN3Yn(n=1 ,2,3) forces at where Fig.(3) shows rapid variation of v(s,) with the distance s for BDM3Y3 and slow variation for BDM3Y1 .This interprets the large error in neglecting the s-dependence produced at R<2 fm. for BDM3Y3 Reid force. In the surface and tail regions() the error produced by neglecting s-dependence is less than 50% because the shape of NN forces at and are almost similar and does not vary strongly with s. For Paris type of NN force shown in Fig.(4), the direct part of BDM3Y3 force is strongly attractive for s<1 fm. then it becomes repulsive. This produces highly attractive HI potential in the inner region for range 0.25 fm. and repulsive potential for range 0.4 fm. The strong variation of BDM3Y3 for small s-values Fig(4a) produces large error between V(R ) and V (R,s) in the inner region. As the distance R increases Fig.(4b) and (4c) show that v(s,) becomes highly repulsive at small s-values and weakly attractive for. This produces weakly attractive total potential in the tail region table(5).

References

1. R.K.Gupta,W.Scheid and W.Greiner, Phys.Rev. Lett. 35(9): 353 (1974).
2.  D.Scharnweber,W.Greiner and W.Mosel,Nuclphys. A 64: 257 (1971
   CrossRef
3. W.Greiner and W.Scheid, J. Phys. Paris32(C6): 91 (1971).
4. H.Holm and W.Greiner, Nucl. Phys.A195:333 (1972) .
   CrossRef
5. R.Sartor,A.Faessler,S.B.Khodkikar and Kerwald, Nucl. Phys. A354,467(1981) .
6.  D.M.Brink and F. Stancu, Nucl. Phys.A243,175(1975); F.Stancu and D.M.Brink, A270: 236 (1976) .
7. M.Ismail, M.Rashdan, A.Faessler, R.linden, N.Ohtsuk and W.Wadia, ibid A490: 715 (1989); M.Ismail, H. Abozahra, Phs. Rev.C53:53 (1996) .
8. J.Blucki,J.Randrup ,W.J.Swiatecki , and C.F.Tsang ,Ann. Phys.(NY), 105: 427 (1977).
   CrossRef
9.  G.R.Satchler and W.G.Love, Phys. Rep.55: 183 (1979).
   CrossRef
10. J.W.Negele and D.Vautherin, Phys. Rev. C5:1472 (1972), C11: 1032(1975).
11. Dao T.khoa, Nucl.Phys. A486 169 (1988).
12.  Dao T.Khoa and W.Von Oertzen, Phys.Lett.304: 8 (1993).
    CrossRef
13. Dao T.Khoa and W.Von Oertzen and H.G. Bolhen,Phys. Rev. Cha: (1994)1652.
14.  Dao T.Khoa and W.Von Oertzen, Phys. Lett.B 342: 6 (1995).
    CrossRef
15. Dao T.Khoa et.al., Phys. Rev. Lett.74: 134(1995).
    CrossRef
16. Dao T.Khoa ,G.R.Satchler and W.VonOertzen, Phys.Rev. C56: 954 (1997).
17. B.Sinha,Phys.Rep. 20: (1975).
18. A.K.Chaudhuri,D.N.Basu and B.Sinha, Nucl. Phys.A43: 415 (1985); A.K.Chaudhuri andB.Sinha ,Nucl.Phys. A455: 169 (1986).
19. S.Misicu and W.Greiner, Phys. Rev.C66:044606 (2002).
    CrossRef
20. M.El.Azab Farid and G.R. Satchler, Nucl. Phys.A438: 525 (1985).
21. D.A. Goldberg et al.,Phys. Rev. C7: 1938 (1973).
22. H.G. Bohlen et al., Z. Phys. A308: 21 (1982).
23. H.G. Bohlen et al., Z. Phys. A322: 241 (1985).
24. E. Stiliais et al., Phys. Lett. B223: 291 (1989).
25. G.Bertsch et.al, Nucl. Phys. A284: 199(1977).
26. A.M.Kobos et al.,Nucl. Phys. A384: 65 (1982);A.M.Kobos et al.,Nucl. Phys. A425: 205 (1984).
    CrossRef
27. M.E.Brandon and G.R.Satchler, Phys. Rep. 285: 14 (1997).
28. W.G.Love and L.W.Owen,Nucl. Phys. A239:74 (1975).
    CrossRef
29. M.Golin,F.petrovich and D.Robson,Phys.Lett. B64: 253 (1976).
    CrossRef
30. M.E. Brandan, M.Rodigueg-Villafuerte and A.Ayala, Phys. Rev. C41: 1520 (1990).
31. M.E. Brandan and G.R. Satchler Phys. Lett. B256: 311 (1991).
    CrossRef
32. H.J.Krappe,J.R.Nix,and A.J.Sierk, Phys. Rev.C20: 992(1979).
33. M.M. Osman, Balkan Phys. Lett. 6: 25 (1998).
34. M. Ismail,M.M. Osman and F. Salah,Phys.Lett. B378: (1996)40;M. Ismail, F. Salah and M.M. Osman,Phys. Rev.C54: 3308 (1996).
35. B.Sinha, and S.A. Moszkowski, Phys. Lett. B81: 289 (1979).
36. A.Faessler,W.H.Dickoff,M.Trefz and M.Trefz and M.Rhoades- Brown, Nucl. Phys. A 428: 2710 (1984).
    CrossRef
37. D.A.Saloner and C.T. Toepffer, Nucl. Phys.A283: 108 (1977).
    CrossRef
38. 38. M.Ismail, A.Y.Ellithi, Choas Solitons and Fractals, 14(9): 1425 (2002)
    CrossRef
39. . X.Campi,and A.Bonyssy, Phys. Lett. B73: 263 (1978)
    CrossRef
40.  J.Phys.G2: 285 (1976)
    CrossRef
41. S.Sartor and F.I.Stancu, Phys. Rev.C29: 1756 (1984).
42. L.G.B.Goldfarb, P.Nagel, Nucl. Phys.A34: 494 (1980).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.