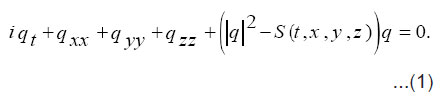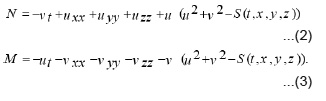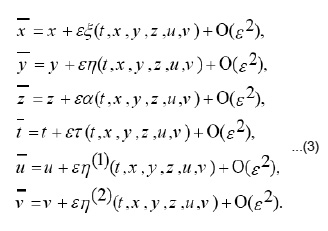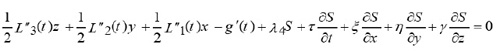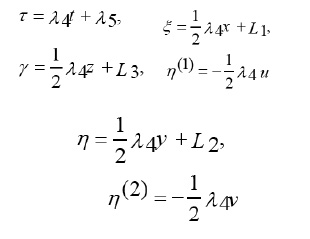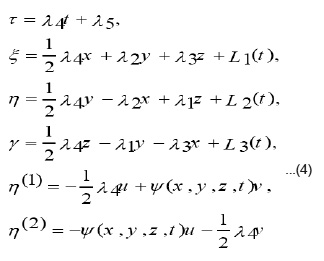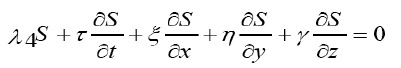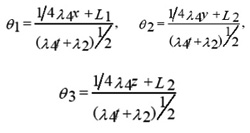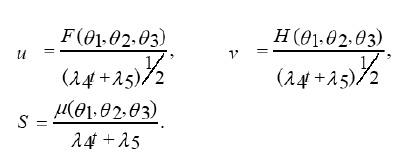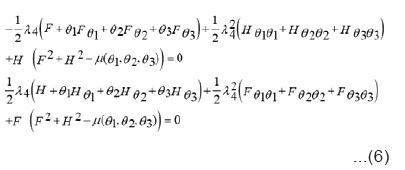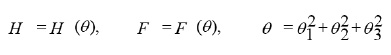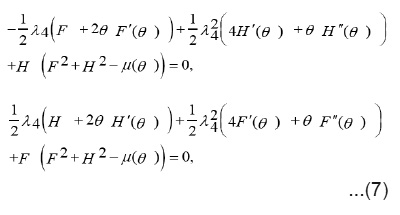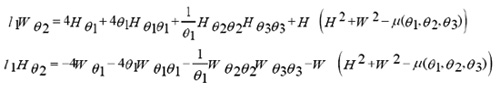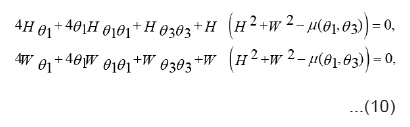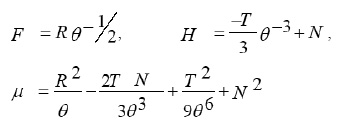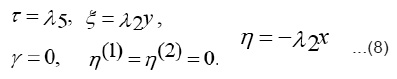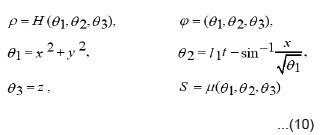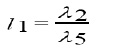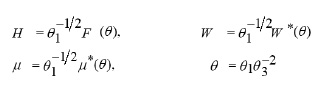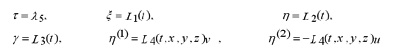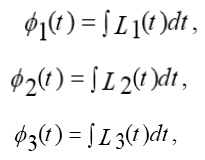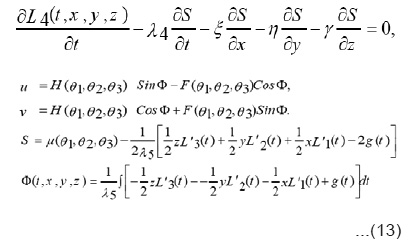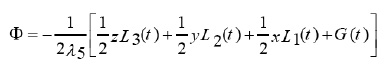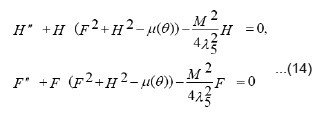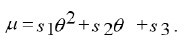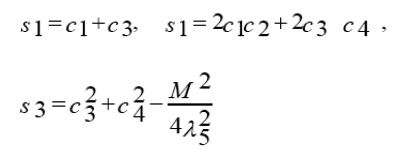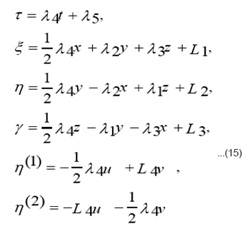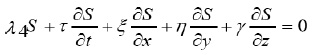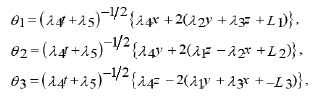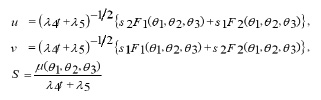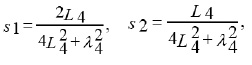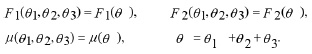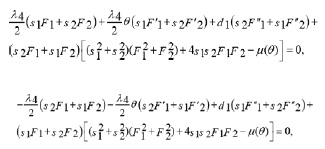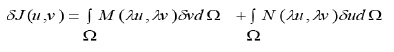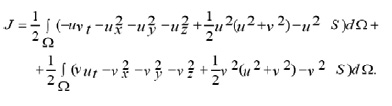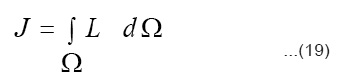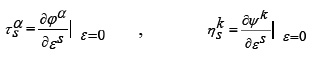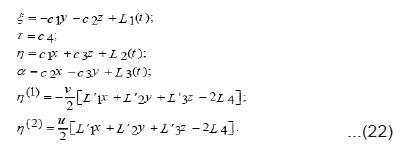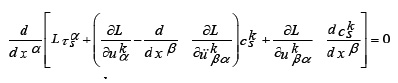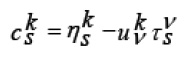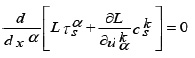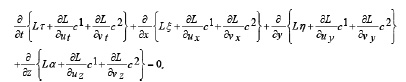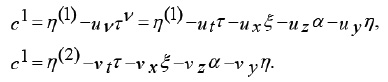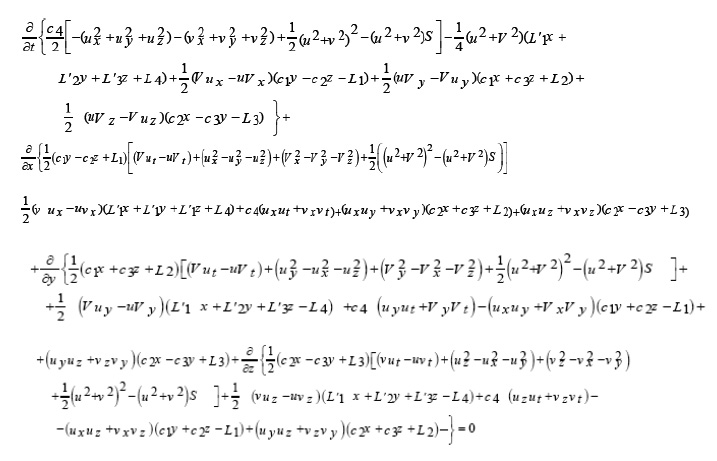Group Analysis and Variational Principle for Nonlinear (3+1) Schrodinger Equation

Introduction

In recent years, a number of works of the symmetry methods are found to be very efficient in applications to differential equations in Physics and Engineering. A subject of a special interest is a study of invariance properties of the equations with respect to local Lie groups point transformations of dependent and independent variables. The importance of the conservation laws lies in the fact that there are situations where numerical schemes have been devised keeping in view the conservation form of the DEs. Also, the conservation law can be used for serving a priori estimates and to obtain integrals of motion, where for certain types of solutions, the conserved density, when integrated, provides us with a constant of motion of the system. Actually, finding the conservation laws of a system is often the first step towards finding its solution. Rund¹ and Logan² have studied the invariance of fundamental functional integral and deduced the first integrals or conservation law for the corresponding system of DEs. The nonlinear (3+1) Schrödinger equation [3, 4] is described by nonlinear couple partial differential equations. It is well know that a part of one parameter symmetry groups of these equations turns out to be their variational symmetries. According to Noether theorem [5, 6] such as invariance of the elementary action is a necessary and sufficient condition of the existence of conservation laws for the Schrödinger equation. Let us consider Schrödinger equation with nonlinear term:

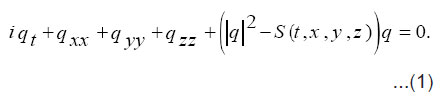
Group Analysis

Equations (1) have some applications in quantum field theory, plasma physics and Engineering [3]. To simplify equation (1), set q =u+iv then, eq. (1) is divided into couple of equations as follows:

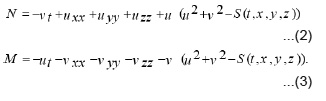
In order to find invariance transformations, we look for infinitesimal Lie point transformations of the form:

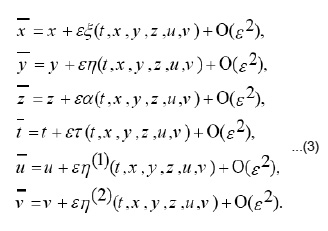
which (2-i, 2-ii) system.

Following the widely used methods in the classical monographs. Concerning these arguments [4-12] we find the coordinates

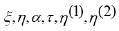
by solving over the determined linear PDE system, usually called the determining system which is obtained by requiring, the invariance of the system (2-i,2-ii) with respect to (3). (1)(2),,,,,……

There are many software packages which aid researchers in obtaining the determining system.

Then we have the following cases:

Case 1

When λ1=λ2=λ3 and Ψ=0 then the infinitesimal take the form

But solving it with arbitrary functions requires analysis. We omit the determining system from which we are able to obtain the following results in the form of the coordinates

and

where, λ₁, λ₂, λ₃ and λ₄ arbitrary constants and L’1(t), L’2(t), L’3(t) are arbitrary functions. Let the function ) S (t, x, y, z,) satisfies the equation and ) S (t, x, y, z,) satisfies the equation:

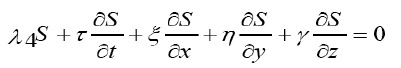
By applying the invariance surface condition, we obtain

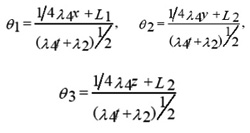
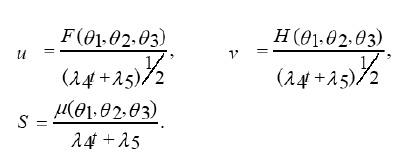
Where λ₁, λ₂, L₁, L₂ are constants and F, H, μ are functions to be determined by substituting ( 4 ) into the system (2-i,2-ii) ,that is ,by solving the following reduced system

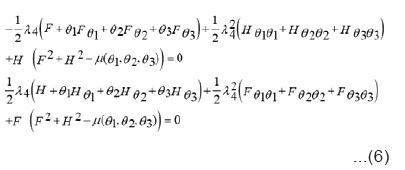
In order to solve system (6), we change the variables

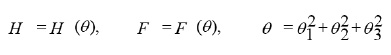
Consequently, the system (6) takes the form:

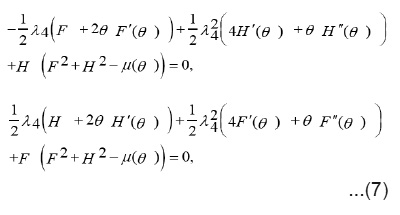
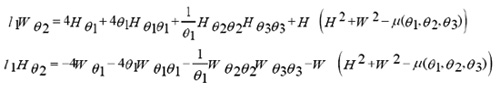
We make use of dilation group and after some manipulations on the system (10) we have

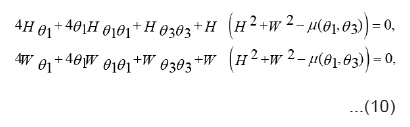
from (7), we have

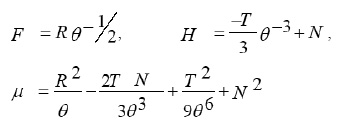
where,,TRN are constants.

Case 2
When λ4=λ3=L1=L2=L3=Ψ=0, then the infinitesimal takes the form

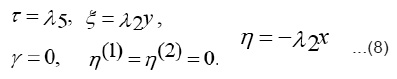
The invariance surface condition may be solved to yield the functional form:

This leads to a reduction of the system (2) in the following form

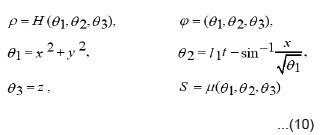
and

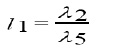
This leads to a reduction of the system (2) in the following form Where

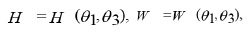
using again dilation group on the system (11) one gets

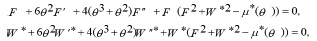
where

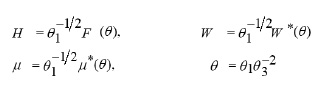
Consequently, system (12) has the solution

when

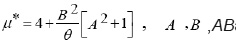
are constants.

Case 3
In this case the infinitesimal takes the form

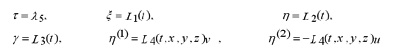
Applying the rules as before (such as case 1, 2), we get:

where

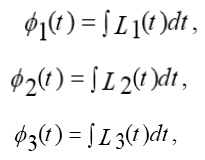
and

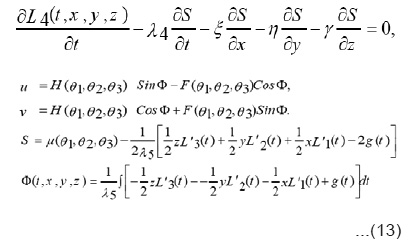
Hence ,

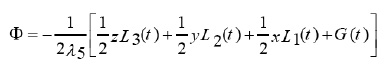
where,

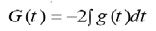
Using the transformation 

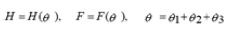
and system (13) in (2), we obtain,

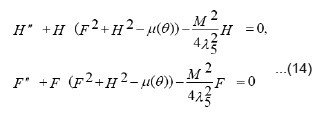
After some calculations on (14), we have the solution in the form:

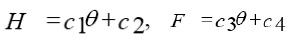
provided that

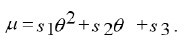
where,

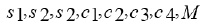
are constants, and

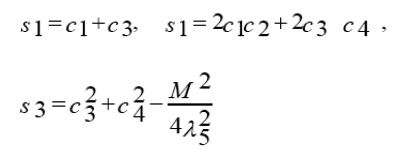
Case 4

When L1(t), L2(t), L3(t) and Ψ(t,x,y,z) are constant, we get

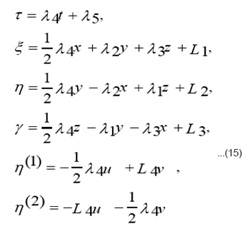
 and

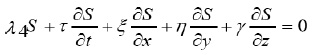
From (15), the invariance surface condition leads to:

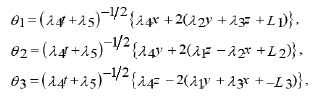
and

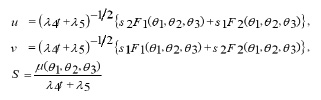
where

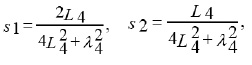
using (16) and changing the variables

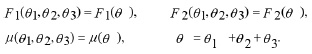
then (2) can be written as the follows

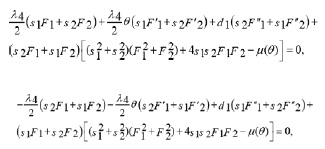
and

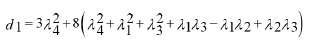
System (16) has the solution

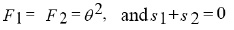
In this case

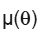
is an arbitrary function.

Variational Principle

In order to study variational principle for our problem,

The system (18) satisfied the consistency conditions for the existence of functional integral. Consequently, a functional integral can be written by using the formula given by Tonti [8, 9] as: ),(vuJ
Since

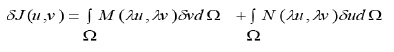
or

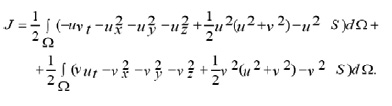
since

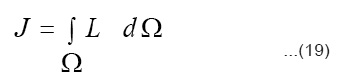
with L being the Lagrangian function, we obtain

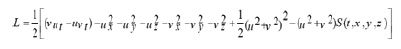
for which the Euler-Lagrange equation is

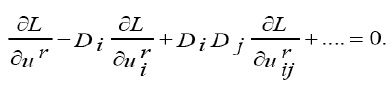
Consequently we have

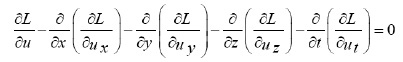
Hence,

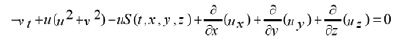
This leads to

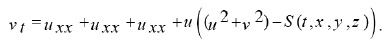
Moreover as,

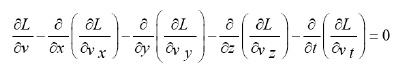
we obtain

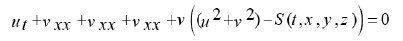
In order to prove the invariance of the fundamental functional integral

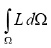
where L is the Lagrangian function and Ω represents the domain of integration to be invariant under the one-parameter group of transformations (3), we can use the following theorem:

Theorem 1 [ 2]
If the fundamental functional integral defined by (19) is invariant under the ƒ{rparameter family of transformation (3), then the Lagrangian L and its derivatives satisfy the ƒ{ridentities:

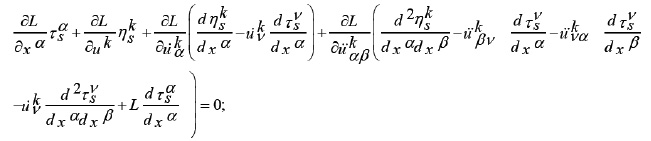
for

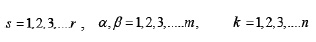
where

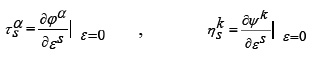
and

Then, Lagrangian and its derivatives must satisfy the condition: L

On Substituting for L and its derivatives in equation (21), we get a polynomial in

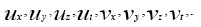
etc Collecting it in descending order of various powers of

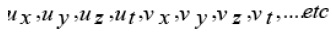
and equating to zero the different powers of

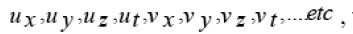
we obtain a system of first order PDEs. On solving this system, we get the following expressions for

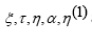
 and n⁽²⁾

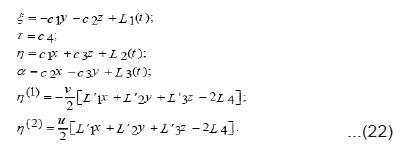
and

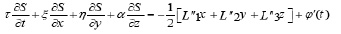
where c1, c2, c3 and 4c are arbitrary constants, but L1, L2, L3 and L4 and φ arbitrary functions of t[12-19].

By using the following theorem

Theorem 2

(Noether‘s Identity)[5,10] Under the hypothesis of theorem 1, the following ƒ{rconservation laws hold true

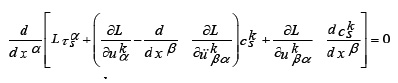
where

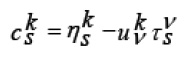
Consequently

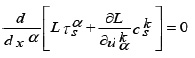
thus , we have

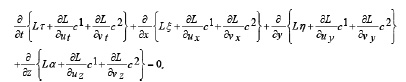
where,

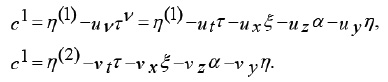
Hence

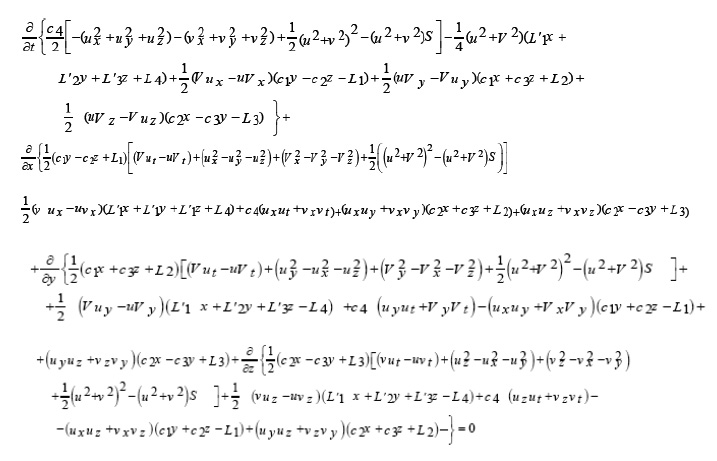
Conclusion

This paper is concerned with finding potentials that admit Lie point symmetries for the nonlinear (3+1) Schrödinger equation, i.e., we give a classification of potentials admitting point symmetries. Finally, we apply Noether’s theorem to show which of this point symmetries are variational and we obtain the corresponding conservation laws

References

1. Rund, H., The Hamilton-Jacobi theory in the calculus of variations. Princeton, NewJersy,(1966).
2. Logan,J.D., Invariant Variational Principles., Academic Press, (1977).
3. Herrera, J.J.E., J.Phys.A:Math.Gen. 17: 95-98 (1984).
4. Cupta, M.R., Physics Lett.,69(3): 172-174(1987).
5. Logan, J., A equations Math., 9: 210-220(1973).
6. Bluman, G., Symmetries and differential equation., Spinger- Ver variational principle lag, New York (1989).
7. P. J. Olver., Applications of Lie Groups to Differential Equations. Springer, New York (1986).
8. Hassan Zedan, Int,J . Non- Linear Mech.,30: 469-489 (1995).
9. Tonti,E., Acad Roy. Belg. Bull. Cl. Sci., 55:137-165 (1969).
10. Tonti,E., Acad Roy . Belg.Bull.Cl.Sci., 55: 262-278 (1969).
11. Logan,J.D.,J. Math. Anal. Appl.,.48: 618-631(1974).
12. Logan, J.D., Noether theorem and calculus of variations. Ph.D. Dissertation, Ohio State University, Columbus (1970).
13. Hassan Zedan, J.Comp. Math. Appl.,32: 1-6(1990).
14. Zayed, E.M.E., Hassan zedan, Int.J .of Nonlinear Science and Numerical Simulation, 5: 221-234 (2004).
15. Zayed, E. M. E., Hassan zedan, Chaos, Solitons and Fractal, 16: 133-145 (2003).
16. Zayed, E.M.E., Hassan zedan, Int.J. Theor. Phys., 40: 1183-1196 (2001).
17. Zayed, E.M.E., Hassan zedan, Chaos,Solitons and Fractal, 13: 331-336,(2002).
18. Zayed, E.M.E., Hassan zedan, Applicable Analysis, 83(11): 1101-1132 (2004).
19. Zayed, E.M.E., Hassan zedan, Applicable Analysis,.84(4): 1-19 (2005).