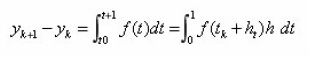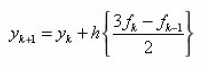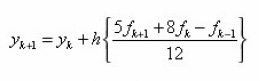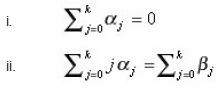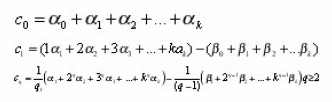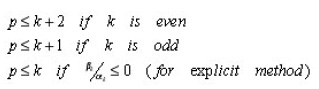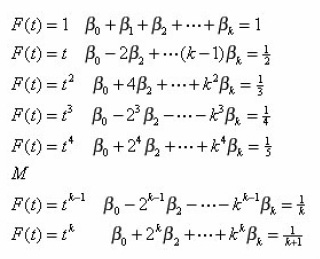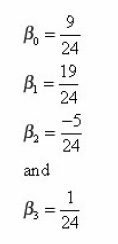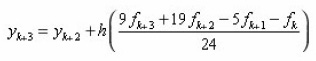A Class of Adams-Like Implicit Collocation Methods of Higher Orders for the Solutions of Initial Value Problems

¹Department of Mathematical Sciences.Nasarawa State University.P.M.B.1022, Keffi, Nigeria. 

²Department of Mathematics and Statistics, Polytechnic of Namibia, Windhoek, Namibia.

DOI : http://dx.doi.org/10.13005/msri/080107

The focus of this research work is the derivation of a class of Adams-like collocation multistep methods of orders not exceeding p=9. Numerical quadrature rule is used to derive steps k= 3,...,8 of the Adams methods. Convergence of each formula derived is established in this paper. As a numerical experiment, the step six pair of the Adams method so derived was used as predictor-corrector pair to solve a non-stiff initial value problem. The absolute errors show an accuracy of o(h⁷).

Introduction

The Adams methods constitute an important class of multistep method for the numerical solutions of ordinary differential equations. In contrast to one-step methods, multistep methods increase efficiency by using the information from several previous solution approximations.

These methods were introduced by J.Couch Adams (1883) for solving problems of capillary action due to Francis Bashforth. Bashforth published his numerical theory and Adams’ numerical method (Goldstine, 1977). They are based on the following idea:

Suppose that the solution y(t) is in fact a polynomial and the function f (t, y) has no explicit dependence on y, then it follows that

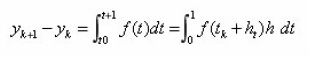
We seek the values of the coefficients β_j so that the corresponding formula has the maximum possible degree of precision. (Note here that the corresponding numerical integration rule would use points from outside the range of integration). A ready example in literature is the popular two-step order two explicit method given as

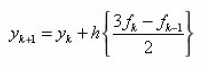
The Adams Moulton methods are solely due to John Couch Adams, like the Adams Bashforth methods. The name of Forest Ray Moulton became associated with the method because he realised that they could be used in tandem with the Adams Bashforth methods as a predictor- corrector pair (Moulton 1926). The two-step order three implicit method is given as.

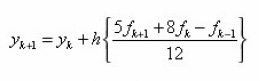
Theorem Due Dahlquist

A linear multistep

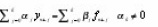
0 method is said to be convergent if it is consistent and zero stable.

A linear multistep method is consistent if it satisfies the conditions below

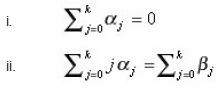
A linear multistep method is said to be zero stable if the roots of the characteristic polynomial

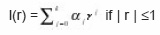
and each root is distinct

Order of Accuracy of Linear Multistep Methods

Equation (2) is said to have order of accuracy p if p is the largest positive integer such that for any sufficiently smooth curve in the rectangular domain D of the first order initial value problem (Equation 1). There exist constants k and h₀ such that for |T_n| ≤ kh^p for 0<h<, for any k+1 points 

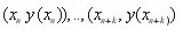
on the solution curve. We can thus deduce that the method (equation 2) is of order of accuracy p if and only if

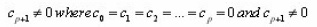
in this case is the error constant.

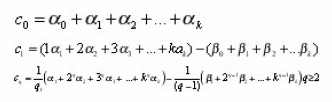
Highest Attainable Order of Stable Multistep Methods

It is a natural task to investigate the stability of the multistep methods with highest possible order. Counting the order conditions shows that for order p the parameters of a linear multistep method have to satisfy p+1 linear equations. As 2k+1 free parameters are involved, (without loss of generality one can assume α_k=1), this suggests that 2k is the highest attainable order. According to Dahlquist (1956), “The order p of a stable linear k –step method satisfies the following conditions:

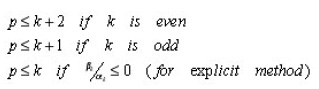
Predictor –Corrector Methods

The idea behind this is that an Adams-Bash forth formulae is used to estimate the value of y(x_k+1) and this is then used in place of y_k+1 on the right-hand side of an Adams- Moulton formula in order to obtain an improved estimate for y_k+1. The Adams Bashforth method is thus used to predict the value y_k+1 and the Adams Moulton formula is the corrector which may be applied iteratively until convergence.

Methodology

For the k- step implicit Adams method, we seek 

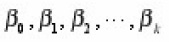
that is F(t) = F(x_k + ht) = 1,t,t²,t³ ,…t^k  

We require 

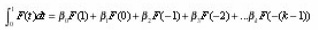
 thus we have the following equations to solve:

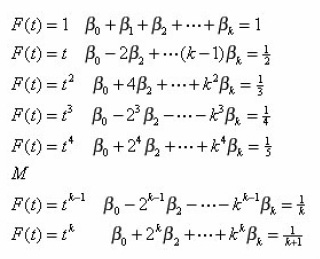
We seek the values of the coefficients β_j so that the corresponding formula has the maximum possible degree of precision.

To confirm this methodology, we show for step k = 3 for the Adams- Moulton scheme as follows:

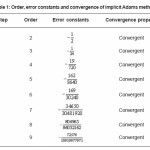
Table 1: Order, error constants and convergence of implicit Adams methods

Click on image to enlarge

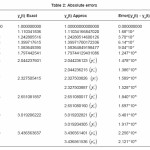
 Table 2: Absolute errors

Click on image to enlarge

For the three – step Adams Moulton method,

We seek

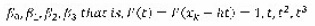
we require

we have the following equations

Solving the martrix equation for

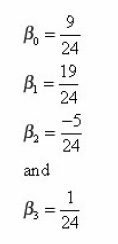
and

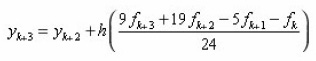
This yields the formula

Following the same procedure we derive the following higher orders:

Stability Accuracy and Convergence Analysis of the Methods

Using the definitions in Section 1, above, the computed order of accuracy, and the convergence analysis of the methods are presented in the table 

It is clear that the methods are of orders k+1 whenever k is the step, and all the methods are convergent.

Numerical Experiment and Results

Example 1

We consider the ivp.

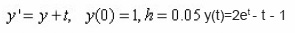
Using the step six order five explicit method below

This work is licensed under a Creative Commons Attribution 4.0 International License.